VaryCHarm: A Method to Automatically Vary the Complexity of Harmonies in Music¶
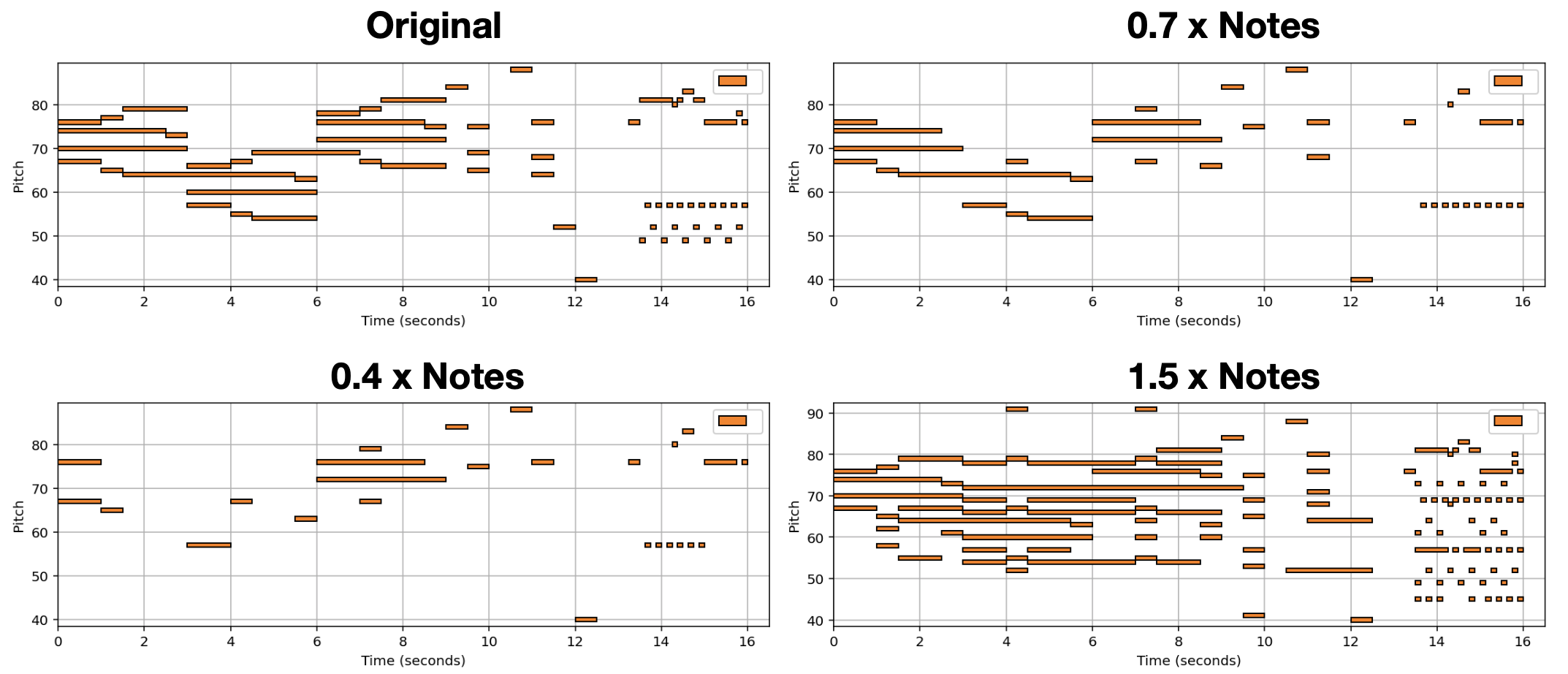
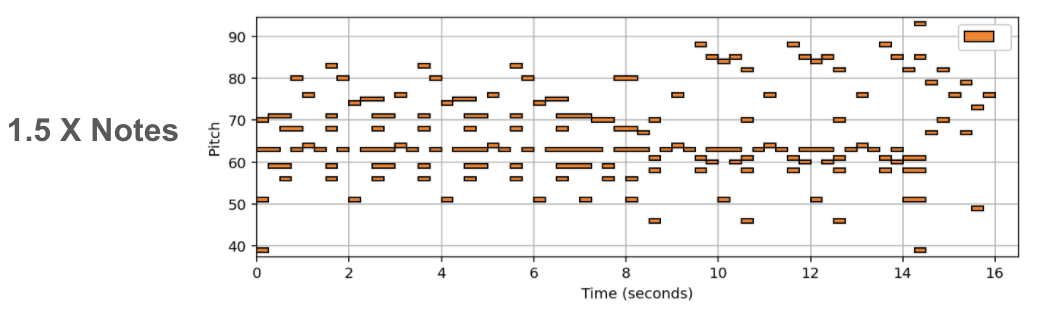
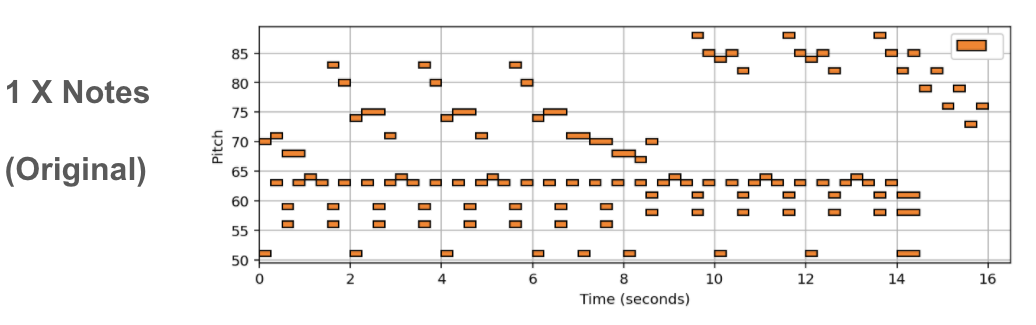
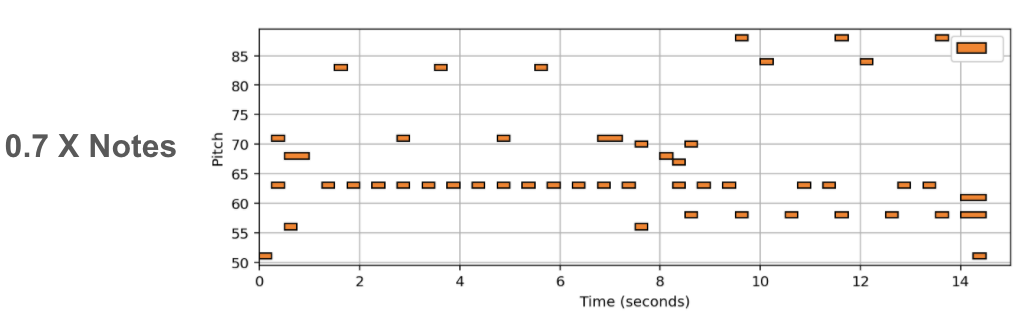
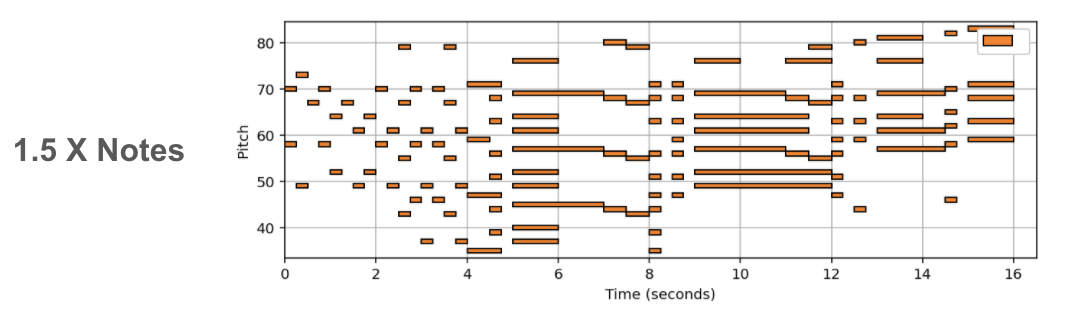
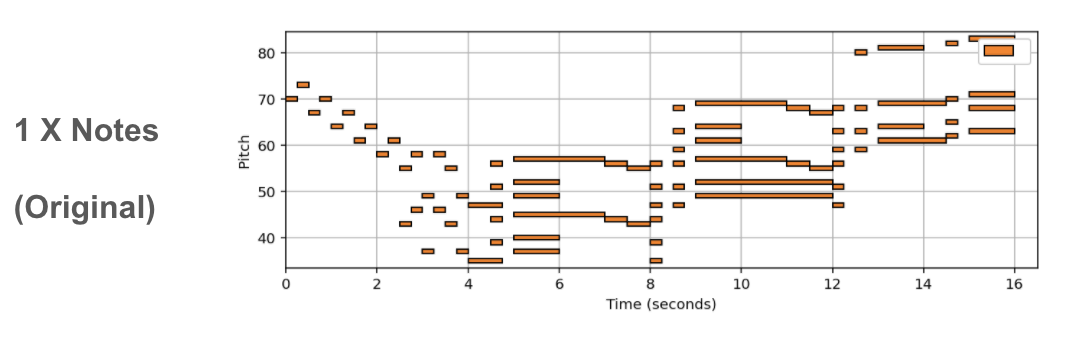
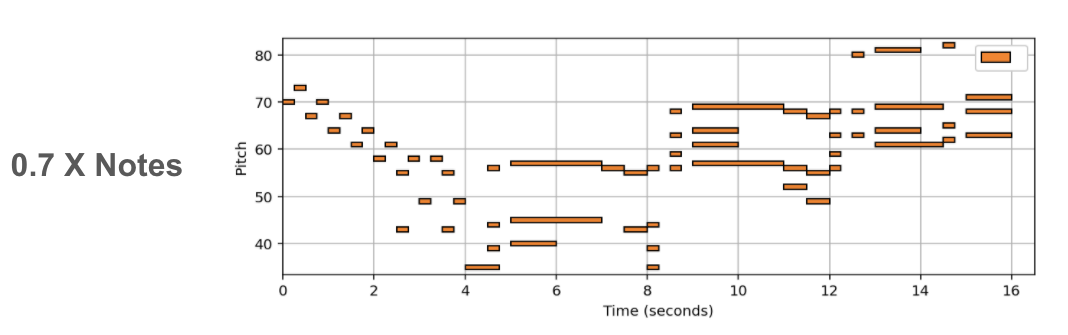
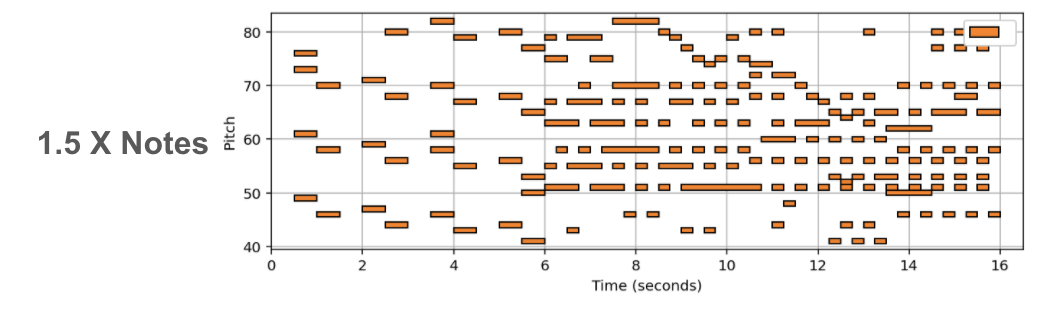
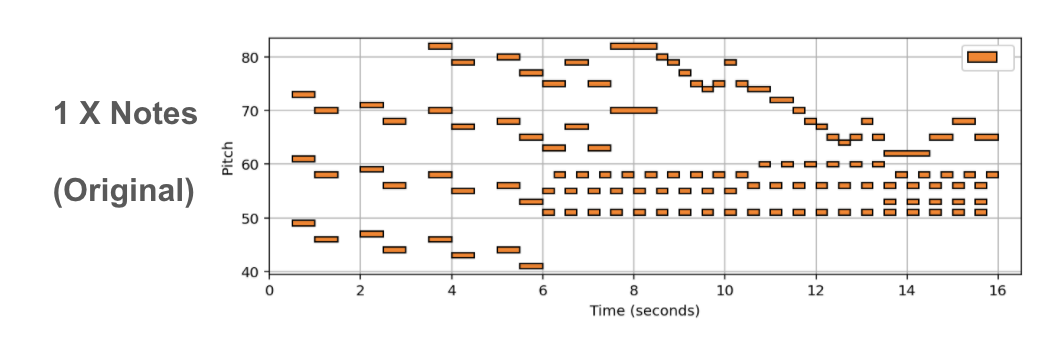
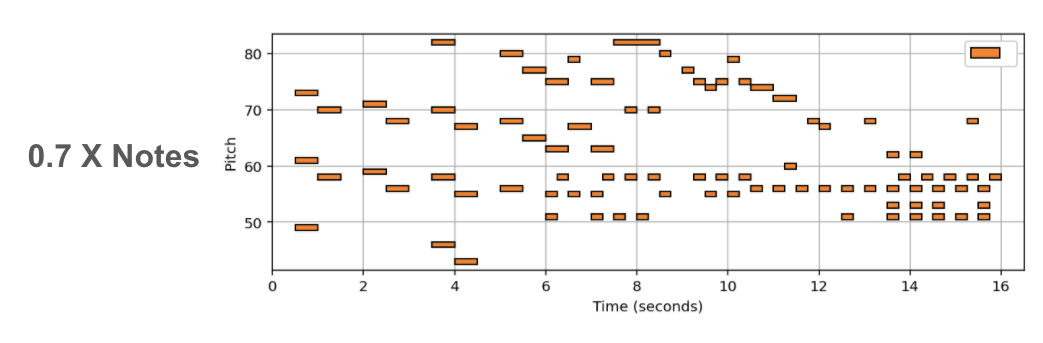
(In Progress) In this post we showcase some results, of a new deep learning method tasked with varying the harmonic complexity of music automatically. In addition, we propose some metrics for evaluation, and design a few baseline based on music theory. I do no discuss the details of the method/implementation since this work is still in progress.
Introduction¶
Music complexity can vary but trained and untrained listeners are still able to recognize the original music. In order to discover a method to vary musical complexity while maintaining we first formulate the problem of varying music complexity and propose a method to preserve general harmonic structure and melody while varying the number of notes. To do this, we find a compressed representation of pitch while simultaneously training on symbolic chord predictions. We test different pitch Autoencoders with various sparsity constraints, and evaluate our results by plotting chord recognition accuracy with increasing and decreasing number of notes, observations in relation to music theory, and by analysing absolute and relative musical features with a probabilistic framework.
Problem Defenition¶
Automatically varying the complexity of music has valuable applications. But how do we approach this problem without supervision? In words, we want to add or remove notes without diverging too much from the original “feeling” of music. In math we write:
The Problem of Varying Harmonic Information:
We denote Symbolic music information as piano rools where the input is information with a fixed history length \(H\) as a matrix \(X_t \triangleq x_{t-H:t} \in \{0,1\}^{P \times H}\). For simplicity, we denote \(\mathcal{X} = \{0,1\}^{P \times H}\) as the input space.
Then the goal is to learn a mapping \(f_\theta(X_t \mid \eta) \rightarrow \hat{X}_t \in \mathcal{X}\) parameterized by \(\theta\) such that \(\hat{X}_t\) summarizes (or further ornament) the original piece of music \(X_t\), given a hyper-parameter \(\eta \in [0,1]\) that controls the sparsity level of \(\hat{X}_t\). More specifically, we consider the following optimization:
\[ \min_{\theta} \mathcal{D}\bigg(f_\theta(X_t \mid \eta),~X_t\bigg) ~~\text{s.t.}~~||f_\theta(X_t \mid \eta)||_0 = \eta HP.\]
Conclusion¶
Empirically our results show we can add or remove notes to existing MIDI music without supervision (or labeled examples). In addition, we can add notes using other intruments for arrangment generation. A more indepth discussion, and evaluation metrics will be added when the full work is presented.